对国内中学生来说，即使最有成就感的学生，微积分这个词也足以令他们心惊胆战。然而，在国际部几乎每个IB/AP小伙伴都会选择挑战微积分，不只是因为它是众多大学专业的基础学科，更是因为我们在学习的过程可以发现身边的数学美，找到数学在现实中的广泛应用。下面，就让我们走进Heather老师和Mark老师的数学课堂！

      在生活中，我们常常看到不同形状的容器。圆滚滚的杯子、精致优雅的香水瓶、小清新的花瓶……

      当我们往这些容器里以恒定的速率灌水，水面增长的快慢遵循什么规律呢？是什么决定了增长的快慢呢？有没有一个公式可以进行计算呢？

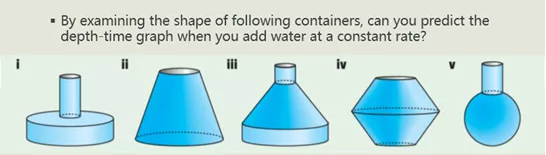
      这就是微积分的第一课。让同学们认识到什么叫做Rate of Change（变化率），并且直观的感受到这种变化在生活中是实在发生，无处不在的。

      中国古代，在没有钟表的时候，就是用盛水的容器来计时。计时器的形状也是千奇百怪的。每个计时器所测量的时间与所对应的刻度其实就是与计时器的形状密切相连。 因为盛满水所用的时间和水面增长的快慢密切相关。只有明白了其中涉及的数学和物理原理，才能够准确地判断时间。

      可见，在我们的生活中，除了最日常的加减乘除计算外，数学知识还可以延展到各个方面，用以帮助我们明白世界形成的原理，并批判地去思考其合理和不合理的地方。

      那么，玄奥的数学是如何与我们现实的世界产生关联的呢？同学们是怎样看到与感受到身边的数学的呢？

      我们通过下面两个例子，来看看我们身边发生着的数学。

     微分方程是微积分中比较困难的内容，原因在于这个方程乍一看像个函数的表达式，但是它和我们学的函数完全不同：理论上，它给出了平面上每一点的方向，实际上，我们没办法把每一点的方向都画出来，只能选择一部分来画图。由于图像缺乏完整性，随意地选取坐标让同学们诚惶诚恐，理解时倍感压力，更不用说去计算它的解了。

      现实生活中，龙卷风的卫星云图就是一个微分方程的例子，在笼罩范围之内，龙卷风在每一点都有一个风向，这就是一个微分方程的完整图形。

      那它的解是什么样子的呢？你只需要丢一片树叶进去，树叶飘过的路线就是它的一个特殊解。你把树叶丢到不同的地方，它就能飘出不同的轨迹。这个区别是因为初始值的不同。树叶被释放的地方，就是它对应的初始值，这就是为啥要先知道初始值才能算出具体的解。

      同学们突发奇想，提出了一个演示的方案：身边找不到龙卷风，但是教室有空调，空调的风将就也是一个向量场，就这样，在我走下讲台的一瞬间，教室里面下了一场纸屑雨，同学们看着漫天飞舞的方程的解，心满意足。

      接下来，在讲到许多微分方程没办法解时，他们不以为然。在他们的学习过程中，见到的都是完美的数学，只有难解和易解，哪有什么不能解？不能解的东西还学来干什么？为了让他们看到微分方程的解虽然存在，却经常找不到，我把一张纸屑放在空调的出风口，叫他们提前画出这张纸屑落地的准确位置，他们慢慢的感受到了这个问题的艰难，逐渐接受了不能解这个现实。

      是的，不只他们，世界上最出色的数学家或者物理学家也没办法画出这张纸落地的准确位置，这就是不可解，至少现在已经有的数学知识中，它是不可解的。

      在同学们刚接触参数方程时，内心是拒绝的。他们觉得已经有了简单可靠，用着得心应手的函数，何必多此一举把简单描述方式搞得那么曲折，何必这样遮遮掩掩的呢？数学的宗旨不应该是让世界变得更清晰明了，简单易懂吗？带着这种迷惑，大家对参数方程爱理不理，直到亲眼看到参数方程做到了许多函数做不到的事情，画出了不是函数图形的形状，才对它强大的描述功能刮目相看。

      下面的三个图形都是运用图形计算器（Graphic Display Calculator）的参数方程画出来的：

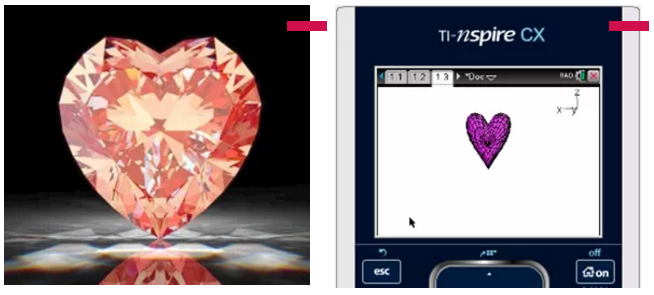
      同学们看到这些形状，立马两眼放光，教室里面炸了锅。行动派的同学立即开始推导这些图形的由来，用刚刚学到的原理把一般方程变成参数方程，再思考怎么让平面图形旋转起来，变成三维的曲面；有同学把心形线也旋转起来了，变成了一个苹果，才发现它们不是同一个类型的形状。看到计算器上失败的“苹果”形状，他们又继续静下心来，跟着老师的提示，思考如何将心形线增加厚度，变成三维的心形。

      同学们见识到了计算器的强大，也认识到了方程的神奇，过了几天，有几个同学给我表演了他们的作品：

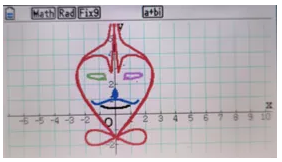
      这个小老头头像是用了10个函数拼接而成，惟妙惟肖。看到同学们把函数玩得这么溜，吓了我一跳，不得不对他们刮目相看。这也让我认识到，同学们具有无限的潜力，只要我们在他们心里播种上数学的种子，并用好奇心来浇灌它，他们会呈现给我们一株参天大树，远超我们的期望。

      数学，一个神圣的名字，它的魔力超乎想象。数学家们常说，数学语言是最美的语言，这是任何一种语言都无法比拟的。当我们静静地欣赏，细细地品味，慢慢地感受，就会发现在我们生活中无处不在的数学美。